Update 25th September 2009: for a very similar picture, see this post by David Eppstein.
[The piece below used to lie around on my homepage since April 2007. I’m slowly closing down that site, as the party is over at Google’s Page Creator.]
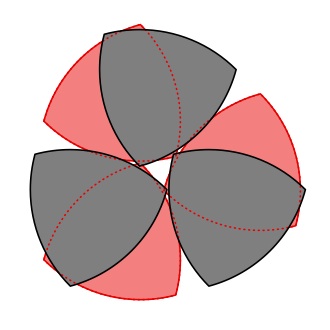
The picture above is something that came out of my work with Achill Schürmann. It is used to disprove a conjecture of Gary Lawlor and Frank Morgan. Each of the grey figures is a Reuleaux triangle. They are all translates of each other. The three sides of a Reuleaux triangle are circular arcs, with the centre of each circle at the opposite vertex of the triangle. The three red figures are obtained by rotating the group of three grey figures by 180 degrees. Note that each grey triangle overlaps each pink triangle. In my opinion it would be quite difficult, using only pencil and paper, to discover a convex figure such that three nonoverlapping translates of it will overlap with each of the three figures obtained by a 180 degree rotation. I found it impossible to do by hand, and had to do a digital drawing, even though I knew theoretically of its possibility. See my paper with Achill for more information.
By the way, the figure was originally programmed in Postscript. More about this later.
Geometry and Combinatorics 